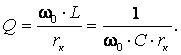Глава 7

ПАССИВНАЯ ФИЛЬТРАЦИЯ КВАЗИСИНУСОИДАЛЬНЫХ СИГНАЛОВ

7.1. Характеристика рассматриваемой задачи

Импульсно-модуляционные способы преобразования параметров электроэнергии – напряжения и тока, как правило, не обеспечивают допустимого уровня их искажений. Для доведения этого показателя до требуемого уровня используют фильтрацию этих величин. На практике чаще всего применяют наиболее простой и достаточно эффективный Г образный LC фильтр. Несмотря на свою простоту модельное описание процессов в нем совместно с реальной активно-индуктивной нагрузкой достаточно сложное. Не случайно решение этой задачи, как в точном, так и в упрощенном виде, интересовало и продолжает интересовать многих инженеров-исследователей. Известно много работ различного ранга – учебников, монографий, статей, посвященных этому вопросу (см., например, достаточно фундаментальную работу [7-1]). Многократное обращение различных исследователей к, на первый взгляд, уже давно решенной проблеме объясняется следующими факторами:

§         многообразием используемых на практике форм фильтруемых сигналов (напряжений, токов), характеризуемых различными спектральными составами;

§         различной (и часто не ожидаемой) реакцией фильтра на различные спектральные составы фильтруемых сигналов, поскольку фильтр может не только ослаблять требуемые высшие гармоники, но некоторые из них и усиливать;

§         сложностью и поэтому недостаточной физической прозрачностью точного модельного описания процесса фильтрации, на основании которого выбираются требуемые значения параметров фильтра – индуктивность его дросселя L и емкость конденсатора С;

§         сложностью получения упрощенного, пригодного для инженерной практики модельного описания, которое было бы достаточно адекватно и приемлемо для различных спектральных составов фильтруемых сигналов;

§         большей склонностью многих исследователей к самостоятельному получению результатов по сравнению с менее творческим процессом проверки адекватности ранее уже кем-то полученных результатов, которая в обязательном порядке необходима и которая к тому же по трудозатратам может оказаться менее эффективной.

Поскольку необходимой основой для самостоятельного формирования модельного описания является глубокое понимание физических процессов, то на первый план выдвигается получение именно этого знания.

7.2. Свойства последовательного LC контура

Очевидно, что для фильтрации выходного напряжения устройства силовой электроники (УСЭ) фильтр должен быть установлен на его выходе. При этом конденсатор фильтра оказывается подсоединенным к выходным выводам УСЭ, к которым подключается нагрузка. На начальном этапе рассмотрим режим холостого хода (ХХ) УСЭ. Г образный LC фильтр в этом режиме превращается в последовательный LC контур.

С целью придания упрощенной методике расчета фильтра физической прозрачности и убедительности ее удобно строить по результатам предварительного исследования свойств последовательного LC контура в виде следующих частотных характеристик:

- зависимостей индуктивного X_L=wL и емкостного X_C=1/wC сопротивлений в функции частоты w: X_L= f(w) и X_C= f(w);

- зависимости результирующего сопротивления контура Z_К=f(w) с учетом его добротности Q=wL/r_к ;

- зависимости напряжения на конденсаторе от частоты w :  U_C=f(w);

- зависимости напряжения на индуктивности от частоты w : U_L=f(w);

- зависимости тока контура от частоты w: I_к= f(w);

- зависимости фазы тока контура от частоты w: j_к =f(w);

- зависимости фазы напряжения на конденсаторе от частоты w : q_С=f(w);

- зависимости фазы напряжения на индуктивности от частоты w : q_L=f(w).

LC контур подключается к источнику переменного напряжения с изменяемой (регулируемой) частотой w :

В контуре протекает ток :

где φ_к – фазовый угол сдвига тока контура относительно питающего контур напряжения (на диаграммах рис.7-1 – 7-3 он обозначается тьакже как угол δ). Заметим, что знак «+» перед углом φ_к соответствует области значений параметра ω* << 1, а знак «–» – области значений ω* >> 1. Графики на рис.7-1 учитывают этот факт, а графики на рис.7-2в следует зеркально отразить снизу вверх.

Использование источника напряжения с переменной частотой позволяет анализировать поведение при фильтрации не только ближайшей высшей гармоники в спектре фильтруемого напряжения, подлежащей ослаблению, но и других высших гармоник., а также основной гармоники.

При изменении частоты w сопротивления X_L и X_C изменяются по возрастающему (линейному) и убывающему (гиперболическому) законам соответственно. При резонансной частоте w = w₀ они оказываются равными, и ток контура достигает максимального значения:

а амплитуды напряжений на конденсаторе и индуктивности увеличиваются в Q раз относительно амплитуды питающего напряжения U_1m, где r_к – активное его сопротивление, а Q – добротность LC контура:

Изменение частоты w (на графиках вышеперечисленных зависимостей) для удобства пользования будем осуществлять в относительных единицах:

 

 

Тогда, резонанс наступает при значении w^*=w₀^*=1.

Из соображений системности изложения материала приведем здесь известные из курса «Теоретические основы электротехники» [7-2] соотношения, подтверждающие справедливость излагаемых положений.

Относительное значение напряжения на конденсаторе:

Здесь U_c и U₁ - действующие (или U_cm , U_1m - максимальные) значения напряжений.

При w^*=w₀^*=1 напряжение на конденсаторе возрастает до значения . Однако максимального своего значения, несколько большего этого и равного:

оно достигает при значении частоты

Напряжение же на индуктивности достигает своего максимального значения при несколько большей частоте:

но при этом имеет такое же значение (7-6):

 

При значении  добротности  резонанс пропадает. Точное значение собственной частоты контура зависит еще и от добротности:

где коэффициент затухания:

Однако на практике у силовых Г образных LC фильтров добротность Q , по крайней мере, больше  4...5, и поэтому допустимая точность достигается и при пользовании приближенной моделью (7-9).

7.3. Методика упрощенного расчета Г образного LC –фильтра

Конечной целью упрощенной методики расчета Г образного LC фильтра является определение значений его индуктивности L и емкости C, которые обеспечивают требуемую степень фильтрации квазисинусоидального сигнала (напряжения). На первом этапе будем определять требуемое произведение этих параметров LC.

7.3.1. Использование последовательного LC контура в качестве Г образного LC фильтра

Последовательный LC контур эквивалентен Г образному LC фильтру в режиме холостого хода (ХХ) преобразователя. Далее анализ работы фильтра и методика его расчета для упрощения ограничиваются рассмотрением лишь только этого режима (ХХ). В ряде случаев инженерной практики такое приближенное определение произведения LC может быть достаточным. При необходимости дальнейшее уточнение его наиболее целесообразно произвести, используя имитационное компьютерное моделирование на сигнальном уровне. При этом задается форма фильтруемого сигнала и на основе вариационного численного эксперимента исследуется прохождение его через LC фильтр в RL нагрузку.

Физическая суть фильтрации (ослабления) высшей гармоники (с частотой w) состоит в следующем: при прохождении через фильтр тока высшей гармоники падение напряжения от нее на индуктивности L должно быть значительно больше, чем на конденсаторе C, который является выходом преобразователя. На частотных характеристиках U_C=f(w) и U_L=f(w) (см. рис.7-2 а, б) требуемое соотношение этих напряжений —

реализуется в области значений w^*>1. Учитывая при этом, что напряжения на индуктивности и на конденсаторе фильтра для конкретной гармоники всегда находятся в противофазе, можно записать

Это соотношение запишем в следующем виде:

Отношение U₁/U_C = К_ОС , по сути, характеризует собой коэффициент передачи (со входа на выход) высшей гармоники частоты w . Поскольку для подавляемой гармоники напряжения значение коэффициента К_ОС должно быть существенно больше 1, то логично обозначить его как коэффициент ослабления (этой гармоники). Выразив в (7-13) напряжения U_L и U_C через сопротивления элементов L и C и через протекающий через них контурный ток I_к, получим выражение для К_ОС:

Реально спектр напряжения, подлежащий фильтрации, содержит основную (первую) гармонику - w₁ и бесконечное число высших гармоник – nw₁ (где n =1; 2; 3;...¥), по частоте в n раз выше основной частоты w₁ (для спектров канонического типа).

Поскольку основная гармоника напряжения фильтром не должна ослабляться, то согласно рис.7-1, рис.7-2 его резонансная частота должна находиться в области:

Какова же при этом будет модель К_ОС для основной гармоники? В области w₁<w₀ (или w^*₁ < 1) напряжение на конденсаторе больше напряжения на индуктивности, поэтому здесь справедливо равенство

Выполнив процедуру, аналогичную (7-14), получим

Необходимо отметить, что при принятых в данном исследовании условиях (допущениях) получается, что согласно (7-17) К_ос(1)<1, то есть для этой гармоники имеет место не ослабление, а ее усиление. Поэтому применительно к ней методически логичнее говорить о коэффициенте передачи

Для n-ой гармоники фильтруемого спектра используемая в (7-14) частота w= nw₁, а модель (7-14) при этом принимает такой вид:

Отсюда определяется необходимое произведение LC:

В дальнейшем будем понимать под номером n номер ближайшей по частоте высшей гармоники.

Полученные модели (7-17) ¸ (7-19) является отправным для определения необходимого произведения LC.

Поскольку в техническом задании на проектирование задается допустимый коэффициент гармоник отфильтрованного напряжения К_Г(U), а не коэффициент ослабления n-ой гармоники К_ОС(n), то нам остается лишь выяснить, как соотносятся между собой эти коэффициенты ( К_ОС(n) и К_Г(U) ).

Решая эту задачу, определим далее насколько (при выбранном К_ОС(n) ) ослабляются гармоники, следующие за n-ой и какое их число целесообразно учитывать при расчете? Найдем коэффициент ослабления для p-ой гармоники (по частоте следующей за n-ой гармоникой) через коэффициент ослабления n-ой гармоники:

Подставив значение LC из (7-19) в (7-20), получим:

7.3.2. Взаимосвязь между коэффициентом гармоник напряжения и коэффициентом ослабления ближайшей высшей гармоники напряжения

Вычисление коэффициента гармоник отфильтрованного напряжения для конкретного спектра напряжения, например, с кратностью частот гармоник относительно частоты основной гармоники, равной (6k ± 1), где k = 1; 2; 3; ... ¥, и с амплитудами гармоник, обратно пропорциональными этому же числу (6k ± 1), производится известным путем:

Здесь для упрощения анализа содержание гармоник в спектре взято в относительных единицах, так что амплитуда основной гармоники оказывается равной 1, а амплитуда (6k ± 1)-ой гармоники меньше ее в (6k ± 1) раз. Ближайшая по частоте гармоника здесь n=5 . Следующие за ней гармоники имеют номера: р₁ = 7, р₂ = 11, р₃ = 13 и т.д. Их коэффициенты ослабления через коэффициент ослабления ближайшей ослабляемой гармоники К_ос(5) вычисляются в соответствии с (7-21). Результаты расчета К_Г(U) представлены в таблице №7-1.

В строках 5, 6, 7 таблицы №7-1 представлены значения коэффициента гармоник отфильтрованного напряжения, вычисленные с разной точностью:

– в строке 5 - с учетом 4-х гармоник: 5-ой, 7-ой, 11-ой, 13-ой;

– в строке 6 - с учетом только 2-х гармоник: 5-ой и 7-ой;

– в строке 7 - с учетом только одной 5-ой гармоники.

Из таблицы следует вывод: для исследуемого спектра напряжения можно ограничиться учетом только одной ближайшей по частоте высшей гармоники. Достигаемая при этом точность менее 5% для предварительных инженерных экспресс-расчетов вполне приемлема.

Таблица №7-1

С учетом этого взаимосвязь (7-22) может быть представлена в таком упрощенном виде:

Уточненный вариант зависимости К_Г(U)= f(К_ос(5)), с учетом 4-х гармоник. для удобства пользования (на основе результатов в строке 5 табл.№7-1) представлен графиком на рис.7-4.

Таким образом, алгоритм определения произведения LC следующий: зная частоту w₁, значение n (в конкретном примере n=5), на основе графика на рис.7-4, приняв требуемое значение К_Г(U) , например К_Г(U)=0,05 и используя получаемое при этом значение коэффициента К_ос(5) = 3,5, находим в соответствии с (7-19) необходимое для фильтрации значение произведения LC.

Аналитическая взаимосвязь (7-19) с учетом упрощенной взаимосвязи (7-23) может быть представлена также в следующем виде:

Как видно, для определения произведения LC здесь вместо коэффициента К_ос(5) требуется знать коэффициент ослабления основной, то есть 1-й гармоники, а не n-ой, то есть в данном случае 5-й. В рассматриваемом примере при К_Г(U)=0,05 согласно графику на рис.7-4 а при К_ос(5) = 3,5 К_ос(1) = 0,82.

Точность модели (7-24) не хуже 5%. Модель (7-24) более информативна, так как одновременно дает представление об изменении содержания основной гармоники напряжения в результате его фильтрации. Напомним, что значение коэффициента ослабления меньше 1 означает, что происходит не ослабление, а усиление гармоники.

Заметим также, что расчетная модель (7-22) справедлива только для тех спектров, у которых амплитуда высших гармоник обратно пропорциональна числу (6Rk ± 1), где R = 1; 2; 3; ...N - канальность нерегулируемых по напряжению инверторов типа RФК-ТИН, причем это же число характеризует собой кратность частоты высшей гармоники относительно частоты основной гармоники. Иной модель будет и в случае регулирования напряжения в инверторе. Для спектров напряжений с различными модификациями ШИМ и для спектров с амплитудно-импульсной модуляцией (АШИМ) модели (7-22) и (7-24) также будут иными, однако общей остается методическая основа для их определения.

Полученные проектные модели хотя и не обеспечивают высокую точность определения требуемого значения LC, однако позволяют оперативно установить разницу в произведении LC для инверторов типа RФК-ТИН с различной канальностью R и на этой основе дать сравнительную оценку этих альтернативных вариантов по массогабаритному показателю.

После определения требуемых значений параметров фильтра L и C делается следующий проектный шаг – конструктивный расчет дросселя индуктивности и выбор типа и номинала конденсатора. Методическое и справочно-информационное обеспечение для решения этих задач можно найти в [6-9], [7-3].

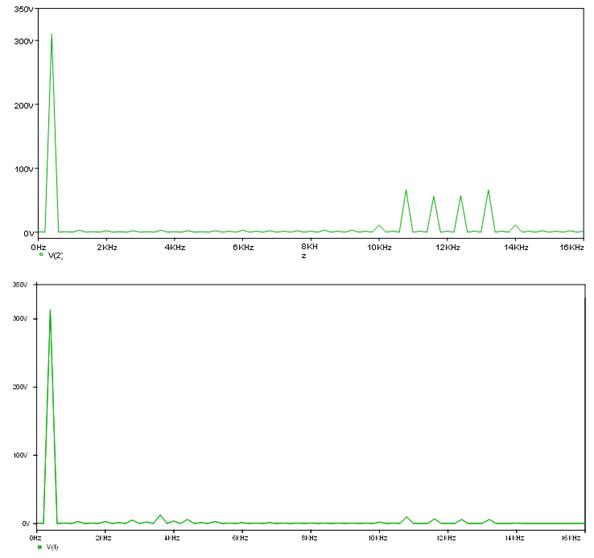
На рис.7-5 в качестве примера приведены осциллограммы фильтрации напряжения с однополярной широтно-импульсной модуляцией (ОШИМ), полученные на основе ИКМ. На рис.7-6 представлены спектрограммы напряжения до и после фильтрации, иллюстрирующие ослабление высших гармоник напряжения. Заметим, что в работах по ИКМ инверторов с ОШИМ выходного напряжения принимал активное участие студент 5 курса Заботин Ю.А.

7.3.3. Поведение LC фильтра в динамике

Покажем, что при разработке преобразователей с выходным фильтром необходимо учитывать поведение фильтра в динамике. Под динамикой будем понимать процессы подключения преобразователя к источнику питания (на холостом ходу и под нагрузкой), процессы наброса и сброса нагрузки, а также процесс его отключения.

Допустим, развертывание СУ заняло некоторое время, и к моменту равному 0, изображенному на рис.7-7, система управления вышла на рабо­чий режим. Если не предусмотрена фиксированная по фазе подача управляющих сигналов на ключи, то процесс заряда конденсатора фильтра может начаться в лю­бой момент времени от 0 до . На рис.7-7 показан наиболее неблагоприятный момент подачи импульсов управления на управляющие входы ключей инвертора, а на рис.7-8 реакция фильтра на такой режим включения. На основную гармонику напряжения накладывается затухающий колебательный процесс с частотой, равной собственной частоте LC контура.

Условия во всех экспериментах следующие: отношение частоты развертывающего сигнала к частоте сигнала задания ξ=30; глубина модуляции μ=1; параметры фильтра L=0.3мГн, C=5.8мкФ; выходная частота 400 Гц.

Подача напряжения на вход фильтра при активной нагрузке

Как видно из осциллограмм на рис.7-9, в сравнении с режимом ХХ время выхода процессов в установившийся режим здесь меньше, искажения выходного напряжения в этом режиме также меньше, однако, перенапряжение в

момент подачи напряжения существенно больше (в 2 раза).

При подаче на вход фильтра напряжения с нулевой фазой переходный процесс полностью исчезает – см. рис.7-10.

 

Подача напряжения на вход фильтра при активно-индуктивной нагрузке

В этом случае при подаче напряжения с неудачной фазой (π/2) перенапряжение на выходе фильтра оказывается еще больше, чем при активной нагрузке, а длительность затухания переходного процесса возрастает.

7.3.4. Векторные диаграммы LC фильтра с нагрузкой

Многомерность и многосвязность процессов в выходной цепи инвертора с фильтром и нагрузкой хорошо иллюстрируется векторными диаграммами на рис.7-12, построенными для основных гармоник напряжений и токов. При их построении использованы следующие параметры:

§         Ф* = ω₂₍₁₎ – коэффициент, пропорциональный установленной мощности фильтра;

§          – волновая проводимость фильтра, отражающая распределение сомножителей C и L в произведении CL;

§          φ₂₍₁₎ – угол между основными гармониками напряжения и тока нагрузки;  – вектор основной гармоники напряжения на входе фильтра;

§          θ₂₍₁₎ – угол между входным – и выходным –векторами напряжений фильтра;

§           – вектор основной гармоники входного тока фильтра (тока через дроссель индуктивности);

§          – угол между векторами  и ;

§         – вектор основной гармоники тока через конденсатор фильтра; – вектор основной гармоники напряжения на конденсаторе.

Примечание: на рис.7-12 векторное обозначение величин (черта сверху) не используется.

Из рассмотрения диаграмм следует, что при одном и том же произведении CL распределение значений между сомножителями C и L играет значительную роль. Необходимо заметить, что конкретное значение параметра Ф*=0,4 соответствует относительно низкочастотным спектрам напряжения, содержащим гармоники, кратность частот которых относительно основной гармоники составляет порядка 5; 7 или 11; 13. Для относительно высокочастотных спектров эта кратность лежит в области нечетных чисел 31÷51, а значения параметра Ф* принимают существенно меньшие значения, порядка 0,05÷0,2 в зависимости от конкретного спектра напряжения, мощности и характера нагрузки и требований к допустимому уровню искажений.

Векторные диаграммы построены по моделям, полученным в [0-1]. Там же приведено достаточно детальное модельное описание процесса фильтрации, на этой основе на ряде примеров проведен анализ и даны рекомендации по проектированию.

Выводы

1. Минимизация значений параметров Г образного LC фильтра представляет собой непростую многомерную, многосвязную задачу, точное аналитическое решение которой (см., например, [0-1], [7-1]) мало приемлемо в инженерной практике (из-за больших трудозатрат и, как правило, жестких временных рамок ее решения).

2. Рассмотренный выше упрощенный способ определения произведения LC следует рассматривать лишь как предварительный этап решения параметрической оптимизации фильтра – как этап определения вектора начальных приближений.

3. Определение требуемого значения произведения LC фильтра еще не является конечным решением задачи его параметрической оптимизации, а является лишь первым этапом. Следующий этап –этап рационального распределения значений L и C в найденном произведении LC. От рационального решения этой задачи зависят такие показатели, как токовая подгрузка инвертора и жесткость его внешней характеристики. Эти показатели заметно влияют на массогабаритные показатели инвертора и на его КПД.

4. Достаточно точное и оперативное решение задачи параметрической оптимизации на этих двух этапах достигается на основе использования имитационного компьютерного моделирования (ИКМ) – современного средства решения подобного рода проектных задач. При этом в качестве вектора начальных приближений целесообразно использовать выше рассмотренную упрощенную методику.

5. Фильтр может оказывать значительное влияние на переходные процессы в инверторе, которые отрицательно влияют на потребителя, если он в момент пуска остается подключенным к инвертору (то есть, к выходу фильтра). С целью повышения надежности потребитель должен подключаться к инвертору после выхода его в установившийся режим.

6. Систему управления инвертором следует строить таким образом, чтобы подача напряжения на вход фильтра обеспечивалась в момент, соответствующий нулевой его фазе. В противном случае на конденсаторе фильтра (и на его индуктивности) появляются перенапряжения, значения которых значительно (вдвое) могут превышать амплитудное значение номинального напряжения и которые могут нарушить электрическую прочность не только самих элементов фильтра, но и потребителей, если они в этот момент подключены.